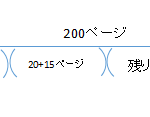小学校低学年で登場する「単位」
ここで意外とつまずく生徒も多いのです。
もし、お子さんが、「単位」を苦手としていると感じたら、必ず対策をしてあげてください。
本当は単位でつまずいているのではなく、別で問題がある可能性もあります。
もくじ
単位は決まりを覚えるだけ

単位そのものは決して難しくありません。
例えば、1時間は60分、1mは100cm、1kgは1000gなどなど、覚えるだけで解決します。
お子さんが、この決まりが分からないといった場合には、力技ではありますが、何度も見て覚えさせてください。これ以外に方法はありません。
覚えても単位の問題は解けない?

1時間は何分ですか?という問題ならば、覚えるだけで解けます。
しかし、問題はそう簡単ではありません。
太郎君は山の頂上まで1kmの道のりを登るのに1時間かかります。お父さんは30分かかります。
一緒にスタートして、お父さんが頂上に着いたとき、太郎君は頂上まで残り何mでしょう?
答え
お父さんが頂上に着くまでに30分かかりますから、太郎君が30分で歩いた距離をまず求めます。
kmをmに直せるか?時間を分に直せるか?をチェックですね。
1kmは1000m 1時間は60分ですから、太郎君は1分間で、1000/60m進みます。30分歩くので、30を掛けて500mです。
1分で何m進むかをどう求めるか?
ここが結構ポイントです。
1時間は60分。これを式にすると1時間=60分。
当たり前じゃないかというツッコミが来そうですが、この意味をしっかり理解しているかが重要なのです。
1時間=60分ならば、60分を1分にするためには、60で割らなければなりません。「=」は同じという意味ですから、60分の方を60で割ったのならば、1時間の方も60で割らなければ「=」になりませんよね。
しつこいですが、下記のような状態です。

別の解き方
お父さんは1kmの山道を30分、太郎君は1時間かかるわけです。
つまり、お父さんは太郎君の2倍のスピードで歩くのです。
別の言い方をすれば、太郎君はお父さんの1/2(半分)のスピードで歩くというわけです。
したがって、お父さんが1Km歩いたとき、太郎君はその半分の地点の500m地点にいます。ですから、残りは500mですね。
単位が問題ではなかった
長々と書いてしまいましたが、気づいていただけたかと思います。
この手も問題は、単位のあたりで出てきそうな問題ですが、お子さんが理解できていないのは単位そのものではなく、出題の中に出てくる、数字と数字の関係や問題そのものの意味が理解できていないのです。
上の例題で言えば、お父さんは太郎君の2倍の速さで歩くという数字の関係。また、お父さんが頂上に着いた=1Km歩いた=30分歩いたという出題文の意味ですね。
ここが理解できていないのに、単位の事ばかりに触れて教えても、問題は解けるようにならないのです。
文章問題そのものの攻略法はこちらを参考にしてください。
いかがでしょうか。
算数には、いろいろな単元(項目)が出てきて、難しく感じますが、お子さんが詰まっているのは、別のところに理由があるかのしれません。
次回も別の例でお話させていただきますね。